Хүмүүс математикийг зөвхөн тоотой холбон ойлгодогоос тоо бодлого, тооны хичээл гэж ч ярьж байдаг. Гэтэл тоо бодох нь зөвхөн математикт ч биш бүхий л хичээлд байдаг шүү дээ. Жишээ нь хими, фикик, түүх, газарзүй гэх мэтээр. Тэгэхээр бусад хичээлийн бодлого, тооцоонууд математикийн тооцоо биш болж таарах уу. Мэдээж үгүй бүхий л тооцоо, бодлогод математикийн ухаанд мөрддөг дүрмийг л ашиглана. Математик хүмүүст тоо бодох гэхээсээ илүү хийсвэрлэн сэтгэх, тунгаан бодох, ухан ойлгох чадварыг өгдөг. Иймээс л математикийн ухааныг бүх ухааны хаан гээд байгаа юм. Математикийн бүх зүйлүүд бие биетэйгээ нягт холбоотой, нэг нь нөгөөгөөс урган гардаг учраас буруу, худлаа зүйл байж болдоггүй нь түүнийг нэг талаас амархан нөгөө талаас хүнд хичээл болгодог.
Математикийн хичээлийн агуулгад багтсан сэдвүүдийг эхнээс нь зөв, сайн ойлгосон бол дараагийн зүйлүүд өмнөхөөсөө урган гарах эсхүл түүнийг ашигладаг тул амархан ойлгогдоно. Эсрэгээсээ суурь ухагдхуунуудыг мэдэхгүй бол шинэ зүйлийг сурах нь бүү хэл ойлгоход ч хүнд болон ирдэг. Иймээс математикийн хичээлийг бүр сууриас нь сайн ойлгон үзэхийг зөвлөе.
Хичээлээр алгебрын тэгшитгэлийг бодоход их хэрэг болдог Виетийн теоремийг авч үзье.
Теорем гэж юуг хэлэх вэ?
Математикийн ямар нэгэн бодлогыг хурдан амар шийдэх зүй тогтолыг хэн нэгэн оллоо гэж бодъё. Үүнийг шууд нээлт гэж үзэж болохгүй. Учир нь тухайн хүний олсон зүй тогтол зөвхөн тодорхой тохиолдолд ажиллаад харин өөр тохиолдолд ажиллахгүй эсхүл бүр буруу ажиллаж ч болно.
Иймээс өөрийн нээлтээ бусдад ойлгуулахын тулд нээсэн зүй тогтолоо нотолгоо хэлбэрээр тодорхойлоод дараа нь түүнийг хөдлөшгүй баримтаар батлах шаардлагатай.
Зүй тогтолын нотолгоо хэлбэрийн тодорхойлолтыг теорем гэж нэрлэдэг. Харин түүний баталгаа нь ямарч маргаан үүсгэхгүй бодон олсон үндэслэл, тооцооноос бүрдэнэ.
Жишээ нь "Энгийн бутархайн хүртвэр, хуваарийг тэгээс ялгаатай ямар нэгэн тоогоор үржүүлэхэд бутархайн утга өөрчлөгдөхгүй" гэдгийг теорем гэж хэлж болно. Хэрвээ тэгээс ялгаатай гэсэн үгийг хасвал энэ нотолгоо нь үржих тоо тэг байхад ажиллахгүй болно. Бутархайн хуваарийг тэгээр үржиж, хуваавал бутархай утгатгүй болдог гэдгийг ч бас нэгэн теорем гэж үзэж болно.
Дээрх нотолгоог математикийн хэлээр бичвэл a/b бутархайн хүртвэр хуваарийг c≠0 тоогоор үржүүлбэл a/b=ac/bc.
a/b=ac/bc тэнцэлийг батлахын тулд порпорцийн 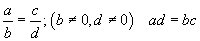 үндсэн чанарыг ашиглавал
үндсэн чанарыг ашиглавал 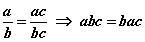 болно.
болно.
Үржигдхүүнүүдийн байрыг соливол үржвэр өөрчлөгдөхгүй аксиомоор 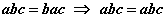 байна. a/b=ac/bc тэнцэл порпорц. Харин порпорц гэдэг нь хоёр харьцааны тэнцэл гэдгээс a/b нь ac/bc тэнцүү нь батлагдана.
байна. a/b=ac/bc тэнцэл порпорц. Харин порпорц гэдэг нь хоёр харьцааны тэнцэл гэдгээс a/b нь ac/bc тэнцүү нь батлагдана.
Виетийн теорем.
Францийн математикч Франсуа Виет эмхэтгэсэн квадрат тэгшитгэлийн коэффициентүүд болон шийдүүд хоорондын сонирхолтой зүй тогтолыг нээсэн. Энэхүү уялдаа холбоог
Эмхэтгэсэн /бүрэн/ x2 + bx + c = 0 квадрат тэгшитгэлийн шийдүүдийн нийлбэр тэгшитгэлийн нэгдүгээр эрэмбийн үл мэдэгдэгчийн коэффициентийг сөрөг тэмдэгтэй авсантай харин шийдүүдийн үржвэр сул гишүүнтэй тэнцүү гэсэн теоремоор тодорхойлжээ.
Өөрөөр хэлбэл эмхэтгэсэн x2 + bx + c = 0 квадрат тэгшитгэл байгаад x1, x2 нь түүний шийд бол 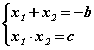
тэнцлүүдийн систем биелэнэ гэсэн үг.
Виетийн теоремийг 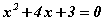 тэгшитгэл дээр харцгаая. Тэгшитгэл ямар шийдүүдтэйг мэдэхгүй ч тэдгээрийг x1, x2 гэж үзье. Тэгшитгэлийн нэгдүгээр эрэмбийн үл мэдэгдэгчийн коэффициент 4 харин сул гишүүн 3 байгаа. Тэгвэл теоремоор
тэгшитгэл дээр харцгаая. Тэгшитгэл ямар шийдүүдтэйг мэдэхгүй ч тэдгээрийг x1, x2 гэж үзье. Тэгшитгэлийн нэгдүгээр эрэмбийн үл мэдэгдэгчийн коэффициент 4 харин сул гишүүн 3 байгаа. Тэгвэл теоремоор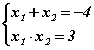 систем гарч ирнэ. Системийг бодоод тэгшитгэлийн шийдүүдийг олж болно. Гэхдээ эмхэтгэсэн квадрат тэгшитгэлийн шийдийг олох
систем гарч ирнэ. Системийг бодоод тэгшитгэлийн шийдүүдийг олж болно. Гэхдээ эмхэтгэсэн квадрат тэгшитгэлийн шийдийг олох 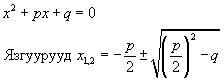 томьёогоор шийдүүдийг олоод теоремийг шалгая. Томьёоны дагуу
томьёогоор шийдүүдийг олоод теоремийг шалгая. Томьёоны дагуу 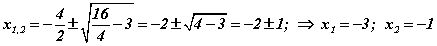 шийдүүд гарна. Теоремийг шалгахын тулд шийдүүдийг тэнцэлүүдийн системд оруулан шалгавал
шийдүүд гарна. Теоремийг шалгахын тулд шийдүүдийг тэнцэлүүдийн системд оруулан шалгавал 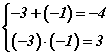 гэж гарснаар
гэж гарснаар 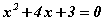 тэгшитгэлийн хувьд теорем үнэн байна.
тэгшитгэлийн хувьд теорем үнэн байна.
Санамж: Нэгдүгээр эрэмбийн үл мэдэгдэгч гэдгийг 1 зэрэгтэй x харин сул гишүүн гэдгийг x -гүй гишүүн гэж ойлгоорой. Үүнийг бид квадрат гурван гишүүнт сэдвээс мэдэн авдаг. Энэ нь математикт бүх зүйлүүд өөр хоорондоо уялдаатай гэдгийн баталгаа. Эдгээр ойлголтыг мэдэхгүй хүнд теоремийн тодорхойлолтыг ойлгоход хүнд болоод ирдэг тул сурагчид x2 + bx + c = 0 тэгшитгэлийн b, c гэх мэтээр автоматаар цээжлэх гэдгээс болоод бодлого бодоход асуудалд ордогийг сануулъя. Томьёоны бичилтэд эмхэтгэсэн кавадрат тэгшитгэлийг ямарч байдлаар бичсэн байж болно. Хичээлийн материалд гэхэд л Виетийн теорем, тэгшитгэлийн шийдийг олох томьёо хоёрт эмхэтгэсэн квадрат тэгшитгэлийг хоёр янзаар буюу коэффициентүүдийг өөр үсгүүдээр тэмдэглэсэн байгаа.
Теоремийг x2 − 2x + 4 = 0 тэгшитгэл дээр авч үзье. Теоремоор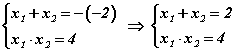 биелэх ёстой. Системд буй тэнцлүүдийг харвал нийлбэр нь 2, үржвэр нь 4 байх тоонууд байхгүй гэдгээс систем шийдгүй тул анхдагч тэгшитгэл шийдгүй болж таарна. Үүнийг
биелэх ёстой. Системд буй тэнцлүүдийг харвал нийлбэр нь 2, үржвэр нь 4 байх тоонууд байхгүй гэдгээс систем шийдгүй тул анхдагч тэгшитгэл шийдгүй болж таарна. Үүнийг 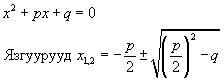 томьёогоор шалгая.
томьёогоор шалгая. 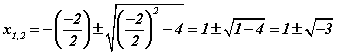 -3 -аас язгуур гарахгүй тул тэгшитгэл үнэхээр шийдгүй нь батлагдана. Энэ тохиолдолд ч Виетийн теорем ажиллаж байна.
-3 -аас язгуур гарахгүй тул тэгшитгэл үнэхээр шийдгүй нь батлагдана. Энэ тохиолдолд ч Виетийн теорем ажиллаж байна.
Санамж: Коэффициент, сул гишүүдийн тэмдгийг оруулж байгаад анхаарна уу. Тэгшитгэлийн нэгдүгээр эрэмбийн үл мэдэгдэгчийн коэффициент -2 тул түүнийг хасах тэмдэгтэй авбал 2 болж байгааг сайн тогтоогоорой.
x2 − 5x + 6 = 0 тэгшитгэлийг аваад үзье. Теоремоор 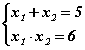 систем үүснэ. Хоёр шийдийн үржвэр 6 байхын тулд шийдүүд хоёулаа эерэг эсхүл хоёулаа сөрөг тоо байх ёстой нь 2 -р тэнцлээс харагдана. Харин 1 -р тэнцлээс шийдүүд сөрөг тоонууд байж болохгүй гэдэг нь тодорхой. Иймээс тэгшитгэлийн шийдүүд эерэг тоонууд байх бөгөөд систем дэхь тэнцлүүдийг хангах тоонууд 2 ба 3 гэдэг нь амархан харагдана. Эндээс тэгшитгэл x1=2; x2=3 гэсэн шийдүүдтэй нь шууд олдоно. Үүнийг өөрсдөө шалгаарай.
систем үүснэ. Хоёр шийдийн үржвэр 6 байхын тулд шийдүүд хоёулаа эерэг эсхүл хоёулаа сөрөг тоо байх ёстой нь 2 -р тэнцлээс харагдана. Харин 1 -р тэнцлээс шийдүүд сөрөг тоонууд байж болохгүй гэдэг нь тодорхой. Иймээс тэгшитгэлийн шийдүүд эерэг тоонууд байх бөгөөд систем дэхь тэнцлүүдийг хангах тоонууд 2 ба 3 гэдэг нь амархан харагдана. Эндээс тэгшитгэл x1=2; x2=3 гэсэн шийдүүдтэй нь шууд олдоно. Үүнийг өөрсдөө шалгаарай.
Санамж: Зарим энгийн тэгшитгэл Виетийн теоремоор тэгшитгэлийг бодохгүйгээр шийдийг олж боломжтой. Шийдүүдийн хувилбар олон байхад энэ арга үр дүн муутайг санаарай.





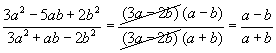

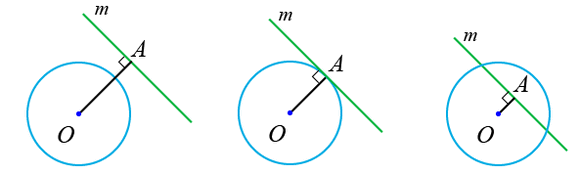
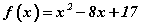 функц өгөгдөв.
функц өгөгдөв.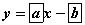

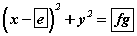
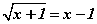 тэгшитгэлийн шийдийг ол.
тэгшитгэлийн шийдийг ол.